Recursos necessários:
– Matlab / Simulink.
Função de transferência:
Uma função de transferência é um modelo matemático simplificado de um processo dinâmico linear (no domínio da frequência – ver Transformadas de Laplace). Uma função de transferência relaciona a saída (resposta) dinâmica de um sistema à entrada (excitação) à qual esse sistema é submetido.
Para representar sistemas dinâmicos reais, em geral, é necessário incluir um atraso de transporte.
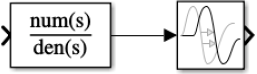
A Figura 01 mostra a representação geral de uma função de transferência. A Figura 02 mostra a representação geral de uma função de transferência com tempo morto.
Importante: “s” (mostrado nas Figuras 01, 02 e 04) é uma variável complexa.
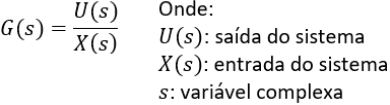
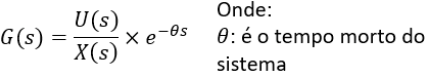
Bloco “Transfer Fcn”:
Para implementar uma função de transferência no Simulink, usa-se o bloco “Transfer Fcn”, mostrado na Figura 03 (bloco à esquerda).
Nas propriedades do bloco tem-se os parâmetros “Numerator coefficients” (numerador da função de transferência) e “Denominator coefficients” (denominador da função de transferência); são nesses dois campos que se colocam os dados referentes à função de transferência.
Bloco “Transport Delay”:
Para implementar uma função de atraso de transporte (tempo morto) no Simulink, usa-se o bloco “Transport Delay”, mostrado na Figura 03 (bloco à direita).
Nas propriedades do bloco tem-se o parâmetro “Time delay”; nesse campo se configura o tempo desejado.
Os blocos “Transfer Fcn” e “Transport Delay” são encontrados na pasta Simulink / Continuous, da biblioteca de funções do Simulink.
Nota: a Figura 04 mostra uma função de transferência, a implementação no Simulink e os devidos parâmetros.
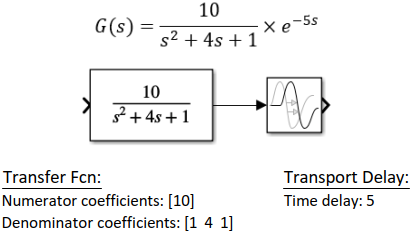
Figura 04
Para baixar essa “Pílula, da LTI” em formato .PDF, acesse nosso servidor. Essa pílula também pode ser acessada no nosso perfil do LinkedIn.
Visite nossa página no Facebook e no Instagram.
–
Elaborado por: Everton Salomé
Referência LTI: PL05-4040-001